Le hashtag #mytoptenbooks était ces derniers jours l’occasion pour chacun et chacune de partager sa sélection de dix livres marquants sur Twitter, Facebook ou Instagram. Après la collecte des 200 premiers top 10, que peut-on dire des choix des participantEs ? MlleFunambuline et Martin Grandjean ont extrait les informations contenues dans les photos, puis un script assez simple a permis la réalisation d’une série de réseaux (biparti, projections sur les auteurs/utilisateurs, etc.).
Voici un bref résumé tiré des deux cent premières listes référencées. L’article que Funambuline en a fait est ici, et celui de Martin ici.
Twitter est un lieu où l’on s’exprime avec un nombre très limité de caractères, de quoi faire deux-trois phrases. Les utilisateurs et utilisatrices y résument une pensée, une idée, ou commentent brièvement la contribution de quelqu’un d’autre. De nouvelles options se sont ajoutées avec le temps, mais Twitter reste un lieu d’éphémère et d’immédiateté. Dans ces conditions, on côtoie les autres tous les jours, à propos d’un ou de plusieurs sujets ; l’image qu’on s’en fait est le plus souvent basée sur les idées, les prises de position, les réactions. Et au final, à moins de faire le pas et de les rencontrer dans la vraie vie, on ne les connaît jamais vraiment. Mais les réseaux sociaux en ligne sont aussi des lieux où les bonnes idées (à vrai dire les mauvaises également) se propagent rapidement et réunissent autour d’elles de petites ou grandes communautés. C’est le cas de l’initiative #mytoptenbooks, lancée par une libraire sur facebook, puis reprise sur Twitter et Instagram. L’idée est simple : réunir dix livres qui nous représentent, nous ont marqués, et en poster une photo. Quand à l’origine de notre démarche, elle est tout aussi simple : considérée indépendamment, une image révèle en ligne une nouvelle dimension de la personnalité de son propriétaire. Prises toutes ensemble, que révèlent-elles ?
Funambuline a réuni ces images dans un storify (elle continue à l’heure qu’il est, donc n’hésitez pas à contribuer). Une fois arrivée à 200 contributions, elle et Martin ont méticuleusement rapporté les noms des utilisatrices et utilisateurs, ainsi que les contenus de leurs collections. Le résultat a ensuite été transformé en un réseau biparti, pour représenter l’ensemble des choix (chaque arête du réseau est un auteur choisi par un utilisateur), ainsi qu’en deux projections, pour visualiser quels auteurs sont cités ensemble, ou quels utilisateurs et utilisatrices ont des goûts proches. Les données ne contiennent pas les noms des ouvrages mais seulement le nom de l’auteur, et plusieurs contributions purement humoristiques ont dû être écartées. Afin d’éviter des surreprésentations aux origines artificielles, un auteur mentionné plus d’une fois par une même personne n’est comptabilisé qu’une seule fois. Après un premier tri, notre échantillon se trouve composé de 1530 choix d’ouvrages, de 158 utilisatrices et utilisateurs, et de 896 auteures et auteurs. Il y a donc des recoupements : plusieurs personnes citent les mêmes auteurs.
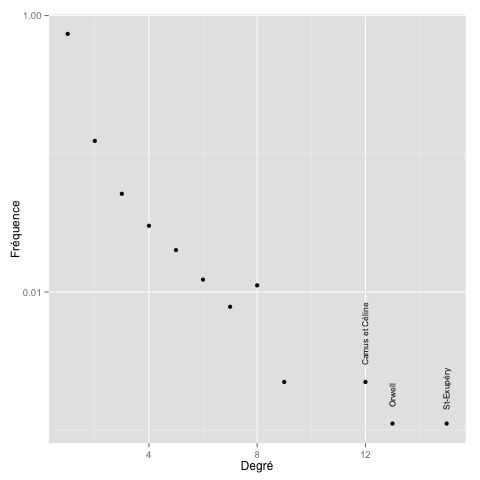
À ce stade, nous voulons savoir quels sont les auteurs les plus populaires, et quelle est la proximité entre les contributions : peut-être que des affinités surgissent. La distribution des citations voit sans surprises quelques auteurs revenir très souvent, mais la grande majorité ne sont cités qu’une voire deux fois. Nous représentons ce résultat dans la figure ci-dessous, où l’échelle logarithmique sur l’axe des abscisses montre cette distribution asymmétrique. Les auteurs plébiscités dans notre échantillon de 158 personnes sont donnés dans le tableau qui suit. Les résultats les plus fréquents correspondent souvent à des oeuvres novatrices, inclassables, et/ou originales. Se démarquer permet de demeurer dans les esprits.

La visualisation d’un réseau biparti (mélangeant auteurs et utilisateurs) de cette taille n’est pas une tâche aisée, ainsi vous m’excuserez de passer cette étape rapidement. Les projections, elles, sont plus pertinentes. Martin a d’ailleurs commencé le travail sur la proximité les auteurs. Le concept de projection tient en une seule idée : si l’auteur A et l’auteur B sont cités par le même utilisateur, alors ils doivent être reliés dans la projection sur les auteurs (qui est un réseau lui aussi). Deux auteurs cités par la même personne ont en effet au moins un point commun. De même, si l’utilisateur A et l’utilisateur B citent le même auteur, ils seront reliés dans la projection sur les utilisateurs, car deux utilisateurs citant le même auteur partagent quelque chose. Voici le réseau montrant toutes les utilisatrices et tous les utilisateurs :

Attention en lisant ce réseau illisible : deux sommets apparaissant côte-à-côte ne partagent pas forcément des auteurs, car le réseau est très dense. Idéalement, il faudrait suivre chaque lien, ce que l’on peut faire facilement à partir des données du réseau, mais difficilement avec la visualisation pour un réseau de cette taille. Une chose est plus sûre par contre : deux personnes diamétralement opposées dans le visuel ont a priori des goûts différents.
Numériquement cette fois, la proximité entre deux utilisateurs peut se calculer par le nombre d’oeuvres partagées. Et cette distance entre deux collections de livres s’obtient par exemple avec le coefficient de similarité de Jaccard. Le principe est, pour tout couple, de calculer le nombre d’ouvrages en commun, puis de diviser par le nombre de leurs auteurs réunis. Par exemple, si la collection de A comprend juste les auteurs W et X, et celle de B les auteurs X, Y et Z, alors la similarité de A et B est :
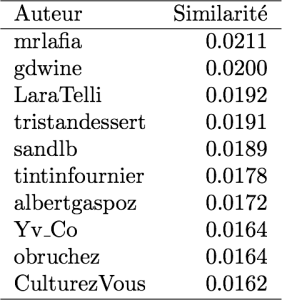
En calculant ce coefficient pour tous les sommets, on découvre que les collections les plus proches (à la toute petite échelle de 10 livres) sont celles de “RM177176” et “rapaubert” partageant Henry Miller, Marcel Proust et Léon Tolstoï (sim. = 0.2), suivis des politiciens de bords opposés Martin Grandjean et Yohan Ziehli (ce que je trouve très amusant), avec une similarité de 0.1875. En calculant la moyenne des similarités, on obtient celles et ceux maximisant cette proximité avec tous les autres utilisateurs :
Ce travail sur la similarité n’a par contre que peu d’intérêt appliqué aux auteurs. En effet, ceux-ci ont toujours au moins en commun les neuf autres auteurs de chaque collection. Dans ce cas, il vaut mieux s’intéresser à une détection des communautés, mais celle-ci n’a rien donné ici, le nombre de collections étant trop petit par rapport au nombre de livres à choisir. Les articles de Martin et Funambuline étudient ce point sur des réseaux réduits, où l’on garde les auteurs ou les liaisons les plus fréquents. Malheureusement, après quelques essais (par exemple sur les auteurs cités au moins trois fois), on découvre que le réseau est trop dense pour voir apparaître de véritables structures : une application de l’algorithme de Blondel et al. (2008) donne une modularité de 0.25, ce qui est trop peu pour affirmer qu’il existe une véritable décomposition de nos goûts en clusters d’auteurs (ce qui est aussi un résultat, mais un peu triste).
Pour terminer cet article, voici mes propres contributions, dont deux sont arrivées trop tard pour faire partie du lot, ce qui n’est pas plus mal, puisque je n’ai pas du tout respecté les règles, quoique… personne n’a dit qu’on ne pouvait pas en proposer deux ou trois, thématiques.
#mytoptenbooks 2/3 pic.twitter.com/BTakPiUDB2
— Yannick Rochat (@yrochat) 27 Avril 2014
#mytoptenbooks 3/3 “fantastique” #totalcheater pic.twitter.com/8AKFr1eqVC — Yannick Rochat (@yrochat) 27 Avril 2014
Mes meilleurs amis/ennemis ces 6 derniers mois #MyTopTenBooks pic.twitter.com/YMuntdMUiX
— Yannick Rochat (@yrochat) 8 Avril 2014
Et n’hésitez pas à contribuer à #mytoptenalbums :
Et vous, quel est votre #MyTopTenAlbums? #musique pic.twitter.com/mtgcMg8e9d
— Xurxo-Adrián Entenza (@xaentenza) 23 Avril 2014
[…] “MyTopTenBooks” chez Funambuline“MyTopTenBooks” chez Yannick Rochat […]